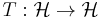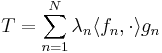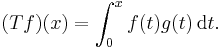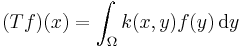Compact operator

In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y. Such an operator is necessarily a bounded operator, and so continuous.

Any bounded operator L that has finite rank is a compact operator; indeed, the class of compact operators is a natural generalisation of the class of finite-rank operators in an infinite-dimensional setting. When Y is a Hilbert space, it is true that any compact operator is a limit of finite-rank operators, so that the class of compact operators can be defined alternatively as the closure in the operator norm of the finite-rank operators. Whether this was true in general for Banach spaces (the approximation property) was an unsolved question for many years; in the end Per Enflo gave a counter-example.

The origin of the theory of compact operators is in the theory of integral equations, where integral operators supply concrete examples of such operators. A typical Fredholm integral equation gives rise to a compact operator K on function spaces; the compactness property is shown by equicontinuity. The method of approximation by finite-rank operators is basic in the numerical solution of such equations. The abstract idea of Fredholm operator is derived from this connection.

1 Equivalent formulations
2 Important properties
3 Origins in integral equation theory
4 Compact operator on Hilbert spaces
5 Completely continuous operators
6 Examples
7 See also
8 Notes
9 References

Equivalent formulations

A bounded operator T is compact if and only if any of the following is true

Image of the unit ball in X under T is relatively compact in Y.
Image of any bounded set under T is relatively compact in Y.
Image of any bounded set under T is totally bounded in Y.
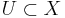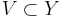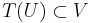there exists a neighbourhood of 0, $U\subset X$ , and compact set $V\subset Y$ such that $T(U)\subset V$ .
For any sequence 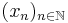$(x_n)_{n\in \mathbb N}$ from the unit ball in X, the sequence 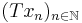$(Tx_n)_{n\in\mathbb N}$ contains a Cauchy subsequence.

Note that if a linear operator is compact, then it is easy to see that it is bounded, and hence continuous.

Important properties

In the following, X, Y, Z, W are Banach spaces, B(X, Y) is the space of bounded operators from X to Y with the operator norm, K(X, Y) is the space of compact operators from X to Y, B(X) = B(X, X), K(X) = K(X, X), 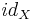$id_X$ is the identity operator on X.

K(X, Y) is a closed subspace of B(X, Y): Let T_n, n ∈ N, be a sequence of compact operators from one Banach space to the other, and suppose that T_n converges to T with respect to the operator norm. Then T is also compact.

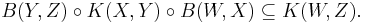$B(Y,Z)\circ K(X,Y)\circ B(W,X)\subseteq K(W,Z).$ In particular, K(X) forms a two-sided operator ideal in B(X).

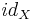$id_X$ is compact if and only if X has finite dimension.

For any T ∈ K(X), 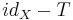$id_X - T$ is a Fredholm operator of index 0. In particular, 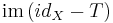$\operatorname{im}\,(id_X - T)$ is closed. This is essential in developing the spectral properties of compact operators. One can notice the similarity between this property and the fact that, if M and N are subspaces of a Banach space where M is closed and N is finite dimensional, then M + N is also closed.

Any compact operator is strictly singular, but not vice-versa.^[1]

Origins in integral equation theory

A crucial property of compact operators is the Fredholm alternative, which asserts that the existence of solution of linear equations of the form

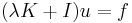
$(\lambda K %2B I)u=f \,$

behaves much like as in finite dimensions. The spectral theory of compact operators then follows, and it is due to Frigyes Riesz (1918). It shows that a compact operator K on an infinite-dimensional Banach space has spectrum that is either a finite subset of C which includes 0, or the spectrum is a countably infinite subset of C which has 0 as its only limit point. Moreover, in either case the non-zero elements of the spectrum are eigenvalues of K with finite multiplicities (so that K − λI has a finite dimensional kernel for all complex λ ≠ 0).

An important example of a compact operator is compact embedding of Sobolev spaces, which, along with the Gårding inequality and the Lax–Milgram theorem, can be used to convert an elliptic boundary value problem into a Fredholm integral equation.^[2] Existence of the solution and spectral properties then follow from the theory of compact operators; in particular, an elliptic boundary value problem on a bounded domain has infinitely many isolated eigenvalues. One consequence is that a solid body can vibrate only at isolated frequencies, given by the eigenvalues, and arbitrarily high vibration frequencies always exist.

The compact operators from a Banach space to itself form a two-sided ideal in the algebra of all bounded operators on the space. Indeed, the compact operators on a Hilbert space form a maximal ideal, so the quotient algebra, known as the Calkin algebra, is simple.

Compact operator on Hilbert spaces

Main article: Compact operator on Hilbert space

An equivalent definition of compact operators on a Hilbert space may be given as follows.

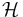
An operator $T$ on a Hilbert space $\mathcal{H}$

$T:\mathcal{H} \to \mathcal{H}$

is said to be compact if it can be written in the form

$T = \sum_{n=1}^N \lambda_n \langle f_n, \cdot \rangle g_n$

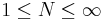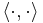where $1 \le N \le \infty$ and $f_1,\ldots,f_N$ and $g_1,\ldots,g_N$ are (not necessarily complete) orthonormal sets. Here, $\lambda_1,\ldots,\lambda_N$ is a sequence of positive numbers, called the singular values of the operator. The singular values can accumulate only at zero. The bracket $\langle\cdot,\cdot\rangle$ is the scalar product on the Hilbert space; the sum on the right hand side converges in the operator norm.

An important subclass of compact operators are the trace-class or nuclear operators.

Completely continuous operators

Let X and Y be Banach spaces. A bounded linear operator T : X → Y is called completely continuous if, for every weakly convergent sequence 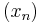$(x_n)$ from X, the sequence 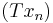$(Tx_n)$ is norm-convergent in Y (Conway 1985, §VI.3). Compact operators on a Banach space are always completely continuous. If X is a reflexive Banach space, then every completely continuous operator T : X → Y is compact.

Examples

For some fixed g ∈ C([0, 1]; R), define the linear operator T by

$(Tf)(x) = \int_0^x f(t)g(t) \, \mathrm{d} t.$

That the operator T is indeed compact follows from the Ascoli theorem.

More generally, if Ω is any domain in Rⁿ and the integral kernel k : Ω × Ω → R is a Hilbert—Schmidt kernel, then the operator T on L²(Ω; R) defined by

$(T f)(x) = \int_{\Omega} k(x, y) f(y) \, \mathrm{d} y$

is a compact operator.

By Riesz's lemma, the identity operator is a compact operator if and only if the space is finite dimensional.

Notes

^ N.L. Carothers, A Short Course on Banach Space Theory, (2005) London Mathemaitcal Society Student Texts 64, Cambridge University Press.
^ William McLean, Strongly Elliptic Systems and Boundary Integral Equations, Cambridge University Press, 2000

References

Conway, John B. (1985). A course in functional analysis. Springer-Verlag. ISBN 3-540-96042-2

Renardy, Michael and Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second ed.). New York: Springer-Verlag. p. 356. ISBN 0-387-00444-0. (Section 7.5)

Kutateladze, S.S. (1996). Fundamentals of Functional Analysis. Texts in Mathematical Sciences 12 (Second ed.). New York: Springer-Verlag. p. 292. ISBN 978-0-7923-3898-7.